section 6.2

Section 6.2 Exponential Functions

An exponential function is a function in which the variable is in the exponent. $y=a^x$ where $a>0$. Remember that exponentiation is repeated multiplication. That is,

$a^n=a\cdot a\cdot a\cdot \cdots \cdot a$ where $a$ is multiplied $n$ times.

Exploring exponential graphs

Play around with this Geogebra activity - move the sliders on the right (they slide up and down) to change the values of the function and see what changes those make to the graph.

https://www.geogebra.org/m/YK6pcUsB

Recall: Rules of Exponents

If $a>0$ and $a\ne 1$:

1. $a^{x+y}=a^x{a}^y$
2. $a^{x-y}=\frac{a^x}{a^y}$
3. $(a^x{)}^y=a^{xy}$
4. $(ab{)}^x=a^x{b}^x$

Calculus facts for exponential functions:

If $a>0$ and $a\ne 1$

1. If $a>1$, then: a. $f(x)=a^x$ is an increasing function. b. ${\displaystyle \underset{x\to -\mathrm{\infty }}{lim}{a}^x=0}$ c. ${\displaystyle \underset{x\to \mathrm{\infty }}{lim}{a}^x=\mathrm{\infty }}$
2. If $0<a<1$, then: a. $f(x)=a^x$ is a decreasing function. b. ${\displaystyle \underset{x\to -\mathrm{\infty }}{lim}{a}^x=\mathrm{\infty }}$ c. ${\displaystyle \underset{x\to \mathrm{\infty }}{lim}{a}^x=0}$

Example

Find the limit ${\displaystyle \underset{x\to \mathrm{\infty }}{lim}{3}^{-x}+1}$

Solution:

The Natural Exponential Function

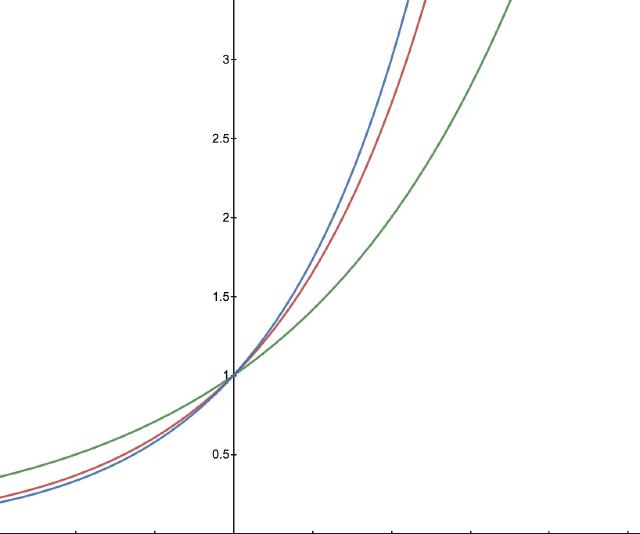Pictured here in green is $y=2^x$, in blue is $y=3^x$, and sitting between them in red is $y=e^x$.

Any exponential function $f(x)=a^x$ has the point $f(0)=1$. However, it becomes very interesting to consider the particular exponential function that has the property that the slope at $(0,1)$ is itself 1. That is, $f^{\prime }(0)=1$ as well. We define this function to be the natural exponential function and call its base $e$:

Define $e^x$ to be the natural exponential function. It has the following remarkable property:

$${\displaystyle \frac{d}{dx}}{e}^x=e^x$$

… it is its own derivative.

Pairing with the chain rule:

$$\frac{d}{dx}{e}^u=e^u{\displaystyle \frac{du}{dx}}$$

Example

Find the derivative of $y=e^{2x}\cos x$

Integration of $e^x$

Since ${\displaystyle \frac{d}{dx}}{e}^x=e^x$, that gives rise to its integral: $$\int e^{x}dx=e^x+C$$

Example

Evaluate $\int x^2{e}^{x^3}dx$