Section 6.1 Inverse Functions
If you’re enrolled in Math/CS 321, see this footnote1
Recall from algebra/precalc/trig:
- A function $f$ is called one-to-one if it never takes the same value twice, that ifs $f(a) \ne f(b)$ if $a \ne b$.
- The Horizontal Line Test A function is one-to-one if and only if no horizontal line intersects a graph more than once.
Inverse Functions
Let $f$ be a one-to-one function with domain $A$ and range $B$, then its inverse function, $f^{-1}$ has domain $B$ and range $A$ and is defined by $$ f^{-1}(y) = x \iff f(x) = y $$ for any $y$ in $B$.
- the domain of $f$ is the range of $f^{-1}$
- the range of $f$ is the domain of $f^{-1}$
that is, the $x$’s become the $y$’s and vice versa.
Finding the inverse of a function: the process:
- Write $y=f(x)$
- Switch the roles of $x$ and $y$ (swap the variables)
- Solve this new equation for the new $y$.
- Write $f^{-1}$ as this function, $y=f^{-1}(x)$
Example
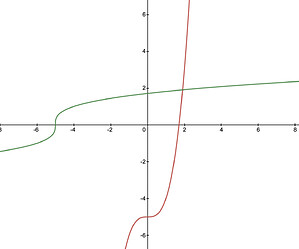
Find the inverse of $f(x) = x^3 - 5$, then graph both $f$ and $f^{-1}$ on the same axes.
Answer
Example
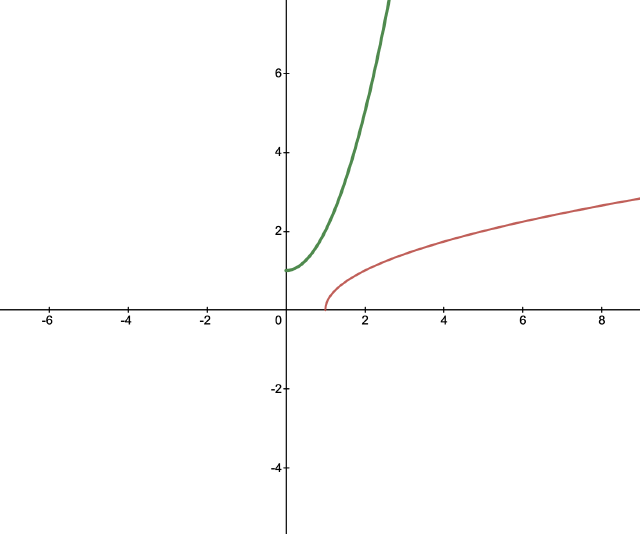
Find the inverse of $f(x) = \sqrt{x - 1}$, then graph both $f$ and $f^{-1}$ on the same axes.
Answer
Takeaway: Inverse function graphs are symmetric over the line $y=x$.
The derivative of inverse functions
If $f$ is a one-to-one function with inverse function $f^{-1}$, and $f’(f^{-1}(a))\ne 0$, then the inverse function is differentiable at $a$ and: $$ (f^{-1})’(a)=\frac{1}{f’(f^{-1}(a))} $$
Example
Consider $f(x) = x^2$ on the restricted domain $[0, \infty)$.
- Show that $f$ has an inverse and that domain.
- Find $(f^{-1})’(1)$ using the above formula.
- Find $(f^{-1})’(4)$ using the above formula.
- Find the inverse of $f$ and show that the computed derivatives match what we expect.
Note that in 321 we define a function by a domain and a codomain. In that context, $f: A \to B$ is invertible if and only if $f$ is both one-to-one (injective) and $f$ is onto (surjective). In calculus we’re just considering the case where $B=f(A)$ and so the functions that we are considering are by their very nature already surjective. That’s why we only need to test injectivity. ↩︎