Section 3.3, The First and Second Derivative Test
Increasing / Decreasing Test
- If $f’(x) > 0$ on an interval, then $f$ is increasing on that interval.
- If $f’(x) < 0$ on an interval, then $f$ is decreasing on that interval.
- If $f’(x) = 0$ on an interval, then $f$ is constant on that interval.
Example
Find where $f$ is increasing and decreasing. $$ f(x) = \frac34 x^4 + 2x^3 - 12x^2 + 5 $$
The First Derivative Test
Suppose that $c$ is a critical number of a continuous function $f$.
- If $f’$ changes from positive to negative at $x=c$, then the function $f$ has a local maximum at $x=c$
- If $f’$ changes from negative to positive at $x=c$, then the function $f$ has a local minimum at $x=c$.
- If $f’$ doesn’t change sign at $x=c$, then $f$ has no local max/min at $x=c$.
Example
Find the local maxima and minima of $f(x) = x + 2\sin x$ on the interval $[0, 2\pi]$.
Concavity
We’ll define concavity on an interval in connection to a function’s shape related to its tangent lines on that interval. But the basic intuitive idea is that a function is:
Concave up if it’s shaped up like a cup ◡
If you poured your favorite beverage into the function, it would hold it. :beer: :grinning_face_with_smiling_eyes:
Concave down if it’s shaped down like a frown ◠
If you poured your favorite beverage into the function, it would spill :droplet: :cry:
Concavity and tangent lines
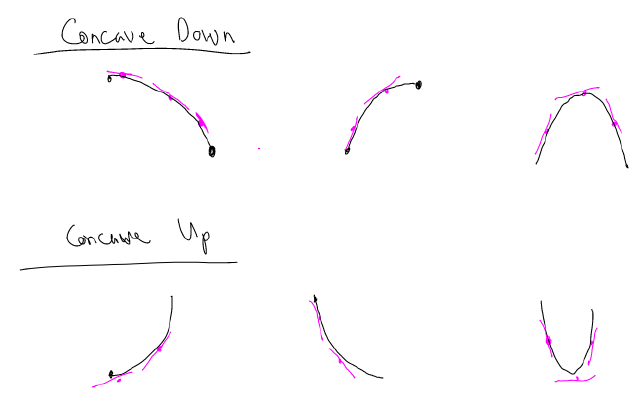
We define a function to be concave up on an interval if the function is always above its tangent lines on that interval.
We define a function to be concave down on an interval if the function is always below its tangent lines on that interval.
Concavity test
- If $f’’(x) > 0$ for all $x$ in an interval, then $f$ is concave upward on that interval.
- If $f’’(x) < 0$ for all $x$ on an interval, then $f$ is concave down on that interval.
A point is called an inflection point if a function is continuous at the point and changes concavity from up to down or down to up at the point.
Example
Find the inflection points and determine the concavity of the function $$ f(x) = x^4 - 2x^2 + 3 $$
The Second Derivative Test
Suppose that $f’’$ is continuous near $x=c$:
- If $f’(c) = 0$ and $f’’(c) > 0$, then $f$ has a local minimum at $x=c$
- If $f’(c) = 0$ and $f’’(c) < 0$, then $f$ has a local maximum at $x=c$.
Note that this uses the second derivative to tell us about extrema. The value $x=c$ is a critical number, but it $f’(c)$ must be defined and 0 at that point.
Example
Find local extrema of the function $$ f(x) = x^4 - 2x^2 + 3 $$
Example
Using concavity, inflection points, and local extrema, sketch a graph of the function $$ f(x) = x^4 - 4x^3 $$