Section 2.2, the derative

The derivative as a function

In the previous section, we found the derivative at a point which is a number.

We will consider the function $f’(x)$ given by: $$ f’(x) = \lim_{h\to 0} \frac{f(x+h) -f(x)}{h} $$ which gives the slope of the tangent line to the function $y=f(x)$ at any point $(x, f(x))$, whenever that limit exists.

Example:

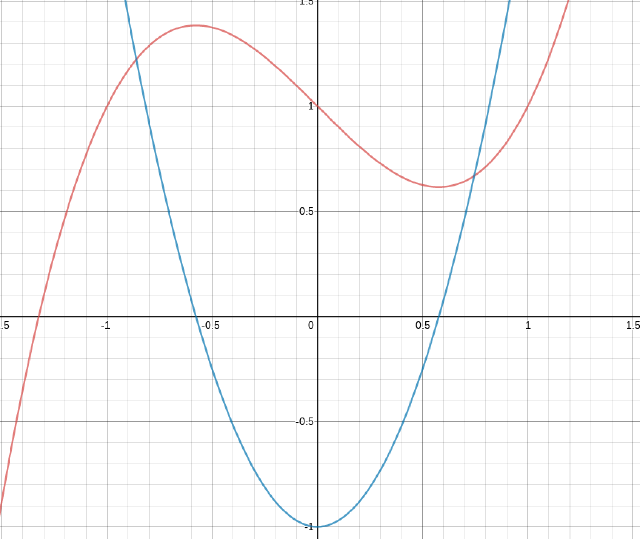
Let $f(x) = x^3 - x + 1$

1. Find the derivative $f’(x)$ of the function.
2. Graph both $f$ and $f’$ on the same coordinate axes.

Here’s the graph

Click to reveal the answer.

Example

Find the derivative of $f(x) = \sqrt{x-1}$ State the domain of $f’$.

Example

Find the derivative of $\displaystyle f(x) = \frac{2+x}{1-x}$

Other Notations

We’ll see many different notations both in this class and outside.

When a function is defined $y=f(x)$, we might write any of the following, which all mean the same thing:

• $f’(x)$
• $y’$ <— this notation we refer to as Newton’s notation¹.
• $\displaystyle \dfrac{dy}{dx}$ <— these are referred to as Leibniz notation²
• $\displaystyle \dfrac{df}{dx}$
• $\displaystyle \dfrac{d}{dx} f(x)$
• $\displaystyle D_x f(x)$ <— you’ll see this in Calc 3 and differential equations
• $\dot{y}$ <— this is actually Newton’s notation from Principia. Physicists often use this in homage to Newton.

If we want to evaluate the derivative of $y=f(x)$ at $x=a$, we can write:

• $f’(a)$
• $\displaystyle \frac{dy}{dx} \Large|_{x=a}$ <— a vertical bar saying “derivative at this number”
• $y’(a)$

As I said above, they all mean the same thing. If you’re ever unsure of notation, please ask!

Differentiability

Definition

A function $f$ is differentiable at $a$ if $f’(a)$ exists. It is differentiable on an open interval (a,b) [or $(a, \infty), (-\infty, b), \text{ or } (-\infty, \infty)$] if it is differentible at every number in the interval.

Example

Polynomials, sine and cosine are nice and differentiable on $(\infty, \infty)$. Their derivatives, for reasons we’ll see later, are still polynomials, -cosine, and sine, respectively, whose domains are all real numbers.

Are there functions that aren’t differentiable?

Example

Where is the function $f(x) = |x|$ differentiable?

When is a function not differentiable?

• Discontinuities

• Cusps

• Vertical tangents.

VIDEO HERE

Higher Derivatives

The second derivative is the derivative of the derivative of a function. For example, if $y=f(x)$, we’ll write:

• The first derivative if $f’(x)$ or $\dfrac{dy}{dx}$.
• The second derivative is $f’’(x)$ or $\dfrac{d^2y}{dx^2}$.

Example:

Let $f(x) = x^3 - x + 1$, find $f’’(x)$

NOTE: we did $f’$ above

Even higher derivatives:

Yes, we’ll go higher. We’ll see 3rd and 4th derivatives (and more in calc 2).

• $f’’’(x)$ is the third derivative <— last of the tick marks
• $f^{(4)}(x)$ is the fourth derivative
• $f^{(5)}(x)$ is the fifth derivative
• … and so on; the parentheses around the number mean derivative not exponent.

Physical interpretation of derivatives?

Velocity is derivative of position with respect to time. …. Acceleration is derivative of velocity with respect to time.

Posting that video might make me seem like a jerk. But that’s $f’’’(x)$³.

Now practice!

Head over to WebAssign and work on section 2.2. If you have questions, post them here, and either I or a fellow student will answer them quickly!