Section 1.7 formal definition of the limit

Neighborhoods

  1. What numbers are within 2 units of 1? Write this as an interval and try completing this inequality: $| x - ? | < 2$

    Click to reveal the answer.$(-1, 3)$. We'll write this as an inequality $|x-1| < 2$

  2. What numbers are within 1/2 of a unit of 1? 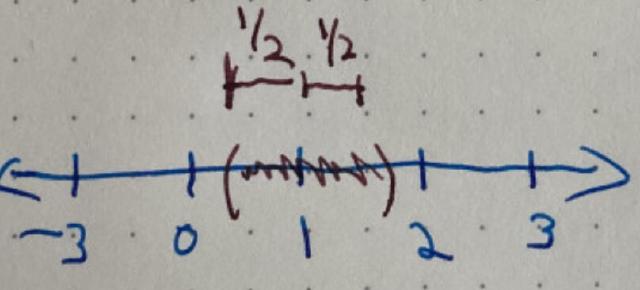Write this as an interval and try completing this inequality: $| x - ? | < 1/2$

    Click to reveal the answer.$\left(\frac12, \frac32\right)$. We'll write this as an inequality $|x-1| < 1/2$

The idea

  • You’re given a function and a particular $x$ value you’re interested in (this value is $a$).
  • Pick a tiny number. 5? Sure. 0.5? Nice. 0.000005? Why not?
    • This number is $\epsilon$.
    • This forms an “epsilon neighborhood” of $y$-values.
  • Now the challenge is to find a corresponding number (most likely similarly tiny):
    • This number is $\delta$
    • This forms a “delta neighborhood” of $x$-values.
  • The limit of the function is $L$ if the function’s $y$-values are always inside the epsilon neighborhood when the $x$-values are in the delta neighborhood (the function always stays within the delta/epsilon rectangle in the picture):

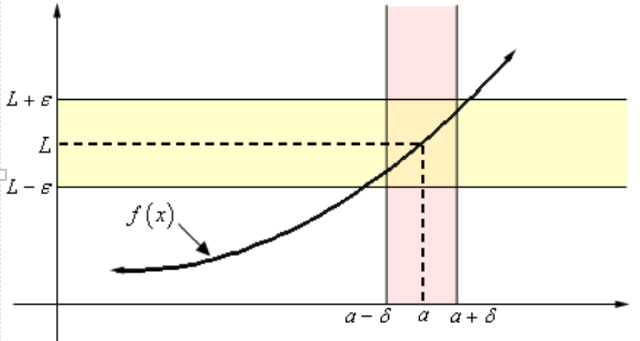
Exploring the idea

Here’s a Geogebra activity to explore the $\delta-\epsilon$ definition of a limit for a function: https://www.geogebra.org/m/QgtVVage

and here’s a video of me describing how this works and our goal.

Formula Definition of the limit

Let $f$ be a function defined on an open interval containing $a$. Then we say that the limit of $f(x)$ as $x$ approaches $a$ is $L$, and we write $$ \lim_{x\to a} f(x) = L $$ if for every $\epsilon > 0$ there is a corresponding number $\delta > 0$ so that if $$ 0 < |x - a| < \delta \text{ then } |f(x) - L| < \epsilon $$

Example

Prove that $\displaystyle \lim_{x\to 4} \left(1 + \frac12 x\right) = 3$

Here’s the formal solution accompanying the work in the video

Click to reveal the answer.Given $\epsilon > 0$, choose $\delta = 2\epsilon$. If $0 < |x-4| < \delta$, then $$ \left|1+\frac12x -3\right| = \left|\frac12 x - 2\right| = \frac12 |x - 4| < \frac12 \cdot \delta = \frac12 \cdot 2\epsilon = \epsilon $$ Thus if $0 < |x-4| < \delta$, then $|(1 + \frac12x) - 4| < \epsilon$. Therefore, by the definition of the limit, $$ \lim_{x\to 4} \left(1 + \frac12 x\right) = 3 $$

Now you try

Prove that $\displaystyle \lim_{x\to 1} \left(2 + 5x\right) = 7$

  1. First, start your “scratch work” and find a value of $\delta$ that will work for any $\epsilon > 0$.

  2. Now your actual solution starts with the text

    Let let $\epsilon >0$ be given, and choose $\delta = $ [your value]. If $0 < |x-1| < \delta$, then …

    and continue like the above example’s solution.

Example

Prove that $\displaystyle \lim_{x\to 0} x^2 = 0$

Note: Along the way, we’ll use the fact that $\sqrt{a^2} = |a|$ for all real numbers $a$.

Now practice!

Head over to WebAssign and work on section 1.7. If you have questions, let me know!