1.6 Limit Laws and the Squeeze Theorem
The limit laws
Suppose $c$ is a constant and the limits: $$ \lim_{x\to a} f(x) \text{ and } \lim_{x\to a} g(x) $$ exist and are finite. Then:
- $\displaystyle \lim_{x\to a} [ f(x) + g(x) ] = \lim_{x\to a} f(x) + \lim_{x \to a} g(x)$
- $\displaystyle \lim_{x\to a} [ f(x) - g(x) ] = \lim_{x\to a} f(x) - \lim_{x \to a} g(x)$
- $\displaystyle \lim_{x\to a} [ cf(x) ] = c \cdot \lim_{x\to a} f(x)$
- $\displaystyle \lim_{x\to a} [ f(x) g(x) ] = \lim_{x\to a} f(x) \cdot \lim_{x \to a} g(x)$
- $\displaystyle \lim_{x\to a} \frac{f(x)}{g(x)} = \frac{\lim_{x\to a} f(x)}{\lim_{x \to a} g(x)}$ if $\lim_{x\to a} g(x) \ne 0$.
- $\displaystyle \lim_{x\to a} [ f(x) ]^n = [\lim_{x\to a} f(x)]^n$ if $n$ is a number
Examples
Below I work many examples in the video
Caution!
The limit laws only work if the limit exists and is finite! For example, we know $$ \lim_{x\to 0} \frac{1}{x^2} = 0 \text{ and } \lim_{x\to 0} \frac{1}{x^4} = 0 $$ but … $$ \lim_{x\to 0} \frac{1/x^2}{1/x^4} = \lim_{x\to 0} \frac{x^4}{x^2} = \lim_{x\to 0} x^2 = 0 $$
The Squeeze Theorem
If $f(x) \le g(x) \le h(x)$ when $x$ is near $a$ $$ \lim_{x\to a} f(x) = \lim_{x\to a} h(x) = L $$ then $\displaystyle \lim_{x\to a} g(x) = L$.
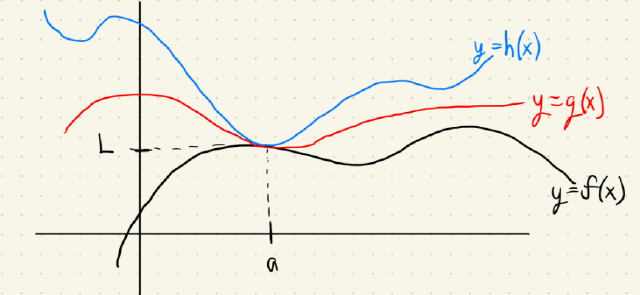
Here’s an illustration of the red function $g(x)$ being squeezed between the upper blue function $h(x)$ and the black function $f(x)$ from below at the point $x=a$.
Example
Show that $\displaystyle \lim_{x\to 0} x^2 \sin\left( \frac{1}{x} \right) = 0$
Working it out in more words:
So, we know that $\sin x$ is always bounded between -1 and 1. It’s range is $[-1, 1]$, right? So let’s start by writing the inequality: $$ -1 \le \sin x \le 1 $$
but it doesn’t actually matter what we plug into the sine function, it’s always bounded, so let’s instead write $\sin (1/x)$ since that’s what we’re given in the question: $$ -1 \le \sin \left(\frac1x\right) \le 1 $$ … that’s still true. Okay, now our question wants us to to find the limit of $x^2 \sin(1/x)$, what can we do to that inequality above to make it look like that? Multiply by $x^2$ everywhere. Note since $x^2$ is not negative, it doesn’t change the inequality signs: $$ -x^2 \le x^2 \sin\left(\frac1x\right) \le x^2 $$
and we wanted to find the limit, so now we apply the limit everywhere there’s an $x$: $$ \lim_{x \to 0} -x^2 \le\lim_{x \to 0} x^2 \sin\left(\frac1x\right) \le \lim_{x \to 0} x^2 $$
and what is $\lim_{x\to 0} x^2$? It’s 0. The limit $\lim_{x\to 0} -x^2$ is also 0, so we have: $$ 0 \le\lim_{x \to 0} x^2 \sin\left(\frac1x\right) \le 0 $$ since we evaluated the limits on the left and right. And since we know that the inner function is bounded above and below by 0, it has to be 0 by the Squeeze Theorem.
Now practice!
Head over to WebAssign and work on section 1.6. If you have questions, let’s talk about them!