Section 1.4, What is Calculus all about?
The Tangent Problem
Tangent comes from the Latin word meaning “touching.” The idea is that given a particular curve and a point, we want to find a line which touching that curve at only that point. We call this the tangent line.
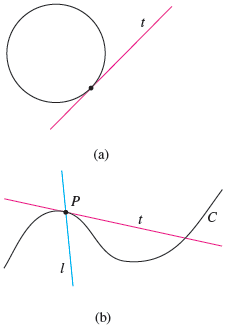
In this picture, part (a), the line $t$ is tangent to the circle. In part (b), the line $t$ is tangent to the curve at point $P$ near that point because near that point, it’s touching the curve at exactly one point. Looking outside the small interval around $P$, though, $t$ does pass through the curve in another place (making it a secant line), so thinking of “tangent” means thinking in a small neighborhood of a point!
Example
Find an equation of the tangent line to the parabola $y=x^2$ at the point $P(1,1)$.
This example is from the textbook, and it looks at computing the slopes of secant lines (thought lines that pass through two points) near point $P(1,1)$. Here’s an excellent Geogebra exploration by WSU faculty Justin Mears which illustrates how the slopes get closer and closer to a particular value (what we’ll call a limit).
Please click this link and and explore the activity:
- You can grab point $Q$ and move it.
- Watch as the secant lines $PQ$ (red) get closer and closer to the tangent line (green), the slope $m_{PQ}$ gets closer and closer to a particular number.
- What is that number?
https://www.geogebra.org/m/c5479ucc
The Velocity Problem
Here we’re asking the question - how fast am I going at this particular moment?
Remember that $\displaystyle \text{Velocity} = \frac{\text{Distance}}{\text{time}}$
Example
Consider a ball thrown in the air, whose height $t$ seconds after it is thrown is given by $s(t) = 40t - 16t^2$ in feet. Compute the average velocity for the time periods beginning at $t = 2$ seconds and lasting 0.5, 0.1, and 0.05 seconds.
Can you estimate the instantaneous velocity when $t =2$?
The Area Problem
We can compute the area of a rectangle really easily. Triangles are basically the same (just 1/2). Straight-edged shapes like stars, pentagons, etc? Easy! Just break them up into triangles and add them together.
It gets a little weirder when shapes are curved. How do we find the area of the bottom picture below?
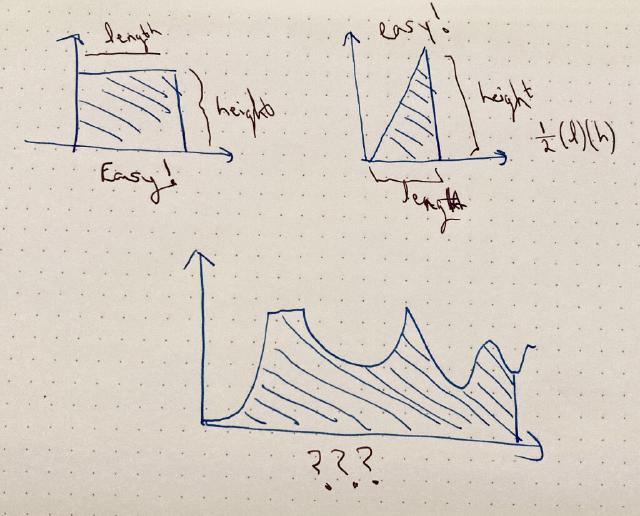
… the idea is that we’ll break it up into smaller shapes (rectangles / triangles) and add those up. But to be accurate, they need to be really, really small rectangles / triangles.
Integral Calculus was developed to answer this question! But it’s not just because we want to find areas.
The Distance Problem
Distance = velocity * time.
In this situation, we know exactly how fast something is going. For example, our car is moving at some velocity $v(t)$. If the velocity is constant (for example, you have set cruise control to 75mph on the I-35), determining how far you go after a certain time is easy.
How far did you travel after 1 hour? 75 miles. After 2 hours? 150 hours. After 90 minutes? 112.5 miles.
What if your velocity varies (e.g. city traffic?). Sometimes you’re accelerating. Sometimes you’re cruising, sometimes you’re stopped at a stop light.
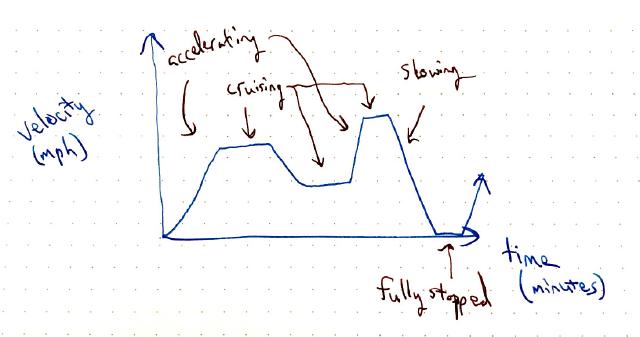
How can we determine how far you traveled? We can break up the time interval into smaller intervals and compute the velocity * time for each interval and then add them up. … this is actually the area problem!
Calculus is so cool!
Have a question? A comment? Want to clarify something above or on your homework set? Send me an email and let’s talk about it!